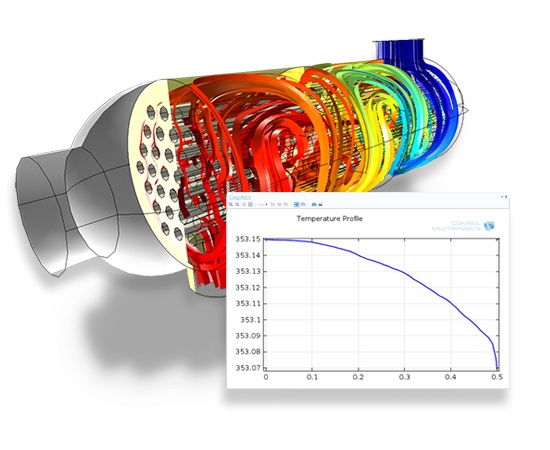
Image made using the COMSOL Multiphysics® software and is provided courtesy of COMSOL.
Temperature profile in the shell-side, and along one of the tubes in a heat exchanger.
The Heat Transfer Module helps investigate the effects of heating and cooling in devices, components, or processes. The module furnishes you with simulation tools to study the mechanisms of heat transfer – conduction, convection, and radiation – often in collaboration with other physics, such as structural mechanics, fluid dynamics, electromagnetics, and chemical reactions. In this context, the Heat Transfer Module acts as a platform for all possible industries and applications where the creation, consumption, or transfer of heat or energy is the focus of or contributes significantly to the studied process.
The Heat Transfer Module comes stocked with an internal material database containing the material properties of a number of common fluids and gases that includes many of the thermodynamic data required for accurate analysis. This includes thermal conductivity, heat capacities, and densities. The Material Library is also a source for material properties, with either the data or algebraic relations of over 2,500 solid materials, where many of their properties, such as Young’s Modulus and electrical conductivity, are temperature-dependent. The Heat Transfer Module also supports the import of thermodynamic and other material data from Excel® and MATLAB®, and for connecting with external thermodynamic databases through the CAPE-OPEN interfacing standard.
This model is intended as a first introduction to simulations of fluid flow and conjugate heat transfer. It shows you how to: Draw an air box around a device in order to model convective cooling in this box, set a total heat flux on a boundary using automatic area computation, and display results in an efficient way using selections in data sets.
Shell-and-tube heat exchangers are commonly used in oil refineries and other large chemical processes. In this model, two separated fluids at different temperatures flow through the heat exchanger, one through the tubes (tube side) and the other through the shell around the tubes (shell side). Several design parameters and operating conditions influence the optimal performance of a shell and tube heat exchanger. This model shows the basic principles of setting up a heat exchanger model. It can serve as a starting point for more sophisticated applications involving parameter studies or additional effects like corrosion, thermal stress, and vibration.
Small heating circuits find use in many applications. For example, in manufacturing processes they heat up reactive fluids. The device used consists of an electrically resistive layer deposited on a glass plate. The layer causes Joule heating when a voltage is applied to the circuit. The layer’s properties determine the amount of heat produced.
This multiphysics example simulates the electrical heat generation, the heat transfer, and the mechanical stresses and deformations of a heating circuit device. The model uses the Heat Transfer interface of the Heat Transfer module in combination with the Shell, Conductive Media DC interface from the AC/DC Module and the Solid, Stress-Strain and Shell interfaces from the Structural Mechanics Module.
This example demonstrates how to model a phase change and predict its impact on a heat transfer analysis. When a material changes phase, for instance from solid to liquid, energy is added to the solid. Instead of creating a temperature rise, the energy alters the material’s molecular structure. Equations for the latent heat of phase changes appear in many texts but their implementation is nonstandard. Heat consumed or released by a phase change affects fluid flow, magma movement and production, chemical reactions, mineral stability, and many other earth-science applications.
This 1D example uses the Heat Transfer in Porous Media interface from the Heat Transfer Module to examine transient temperature transfer in a rod of ice that heats up and changes to water. In particular, the model demonstrates how to handle material properties that vary as a function of temperature.
This model proceeds as follows. First, estimate the ice-to-water phase change using the transient conduction equation with the latent heat of fusion. Next, compare the first solution to estimates that neglect latent heat. Finally, run additional simulations to evaluate impacts of the temperature interval over which the phase change occurs.
This study simulates the thermal behavior of a computer Power Supply Unit (PSU). Most of such electronic enclosures include cooling devices to avoid electronic components to be damaged by excessively high temperatures. In this model, an extracting fan and a perforated grille cause an air flow in the enclosure to cool internal heating.
This example demonstrates how to model phase transition by a moving boundary interface according to the Stefan problem. A square cavity containing both solid and liquid tin is submitted to a temperature difference between left and right boundaries. Fluid and solid parts are solved in separate domains sharing a moving melting front. The position of this boundary through time is calculated according to the Stefan energy balance condition. In the melt, motion generated by natural convection is expected due to the temperature gradient. This motion, in turn, influences the front displacement.
In massive forming processes like rolling or extrusion, metal alloys are deformed in a hot solid state with material flowing under ideally plastic conditions. Such processes can be simulated effectively using computational fluid dynamics, where the material is considered as a fluid with a very high viscosity that depends on velocity and temperature. Internal friction of the moving material acts as a heat source, so that the heat transfer equations are fully coupled with those ruling the fluid dynamics part. This approach is especially advantageous when large deformations are involved.
This model is adapted from a benchmark study. The original benchmark solves a thermal-structural coupling. The alternative scheme modeled here couples non-Newtonian flow with the heat transfer equations. In addition, because it is useful to know the stress in the die due to fluid pressure and thermal loads, the model adds a structural mechanics analysis to the other two.
A comparison between the available experimental data and the numerical results of the simulation shows good agreement. On the basis of the results from the simulation, the engineer can improve the preliminary die design by adjusting relevant physical parameters and operating conditions.
Evaporation in porous media is an important process in the food and paper industries, among others. Many physical effects must be considered: fluid flow, heat transfer, and transport of participating fluids and gases. All of these effects are strongly coupled and predefined interfaces can be used to model these effects with the Heat Transfer Module.
This tutorial model describes an arbitrary case of drying a wet porous object using laminar air flow. The air is dehumidified at the inlet to the porous object where its moisture content increases as it flows through the porous medium. The model focuses on the steps required to implement simulate multiphase flow in porous media, in the Heat Transfer Module, together with the evaporation of the liquid to a gaseous phase. Water saturation in the porous medium is computed over time.
Thermoelectric coolers are widely used for electronics cooling in various application areas, ranging from consumer products to spacecraft design. Exploiting the Peltier effect, they consist of several thermoelectric legs sandwiched between two thermally conductive plates, one cold and one hot. Due the variety of applications, there can be many different thermoelectric cooler configurations.
The Thermoelectric Cooler app covers the basic design of a single-stage thermoelectric cooler of different sizes with different thermocouple sizes and distributions. You can use the app to help find the best thermoelectric cooler for a specific application. Manufacturers can also use it to optimize designs and provide application-related performance values. Additionally, the app serves as a starting point for more detailed calculations with additional input options and can be extended to multistage thermoelectric coolers.
This is done by varying the geometric parameters of the different components of the thermoelectric cooler, the material that makes up the thermoelectric legs, and some operating conditions.
The suite of models examine the air cooling of circuit boards populated with multiple integrated circuits (ICs), which act as heat sources. Two possible cooling scenarios are depicted: vertically aligned boards using natural convection, and horizontal boards with forced convection (fan cooling). In this case, contributions caused by the induced (forced) flow of air dominate the cooling. To achieve high accuracy, the simulation models heat transport in combination with the fluid flow.
The example models the heat transfer of a circuit-board assembly using the Heat Transfer Module’s Conjugate Heat Transfer predefined multiphysics coupling. The modeled scenario is based on work published by A. Ortega.