Image made using the COMSOL Multiphysics® software and is provided courtesy of COMSOL.
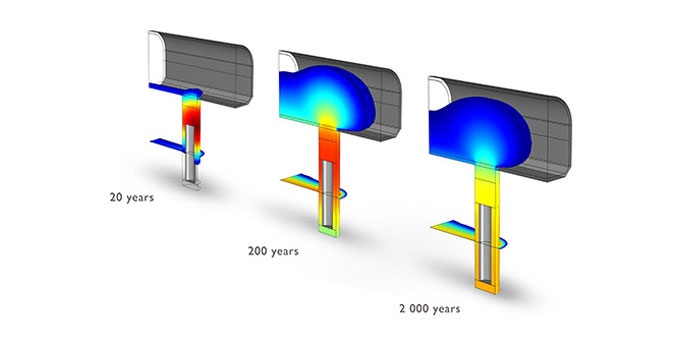
Nuclear waste repositories are now being built to store spent fuel rods for the next one hundred thousand years or so. This model shows a hypothetical case where a breach in the fuel bundle canister leads to leakage through a fracture in the surrounding rock and backfill in the tunnel above.
The Subsurface Flow Module is for engineers and scientists who want to simulate fluid flow below ground or in other porous media and also connect this flow with other phenomena, such as poroelasticity, heat transfer, chemistry, and electromagnetic fields. It can be used for modeling groundwater flow, the spread of waste and pollution through soil, the flow of oil and gas to wells, and land subsidence due to groundwater extraction. The Subsurface Flow Module can model subsurface flow in channels, saturated and variably saturated porous media, or fractures, and couple these to simulations of solute and heat transport, geochemical reactions, and poroelasticity. Many different industries need to deal with challenges within geophysics and hydrology. Engineers from the fields of civil, mining, petroleum, agricultural, chemical, nuclear, and environmental engineering often need to consider these phenomena as the industries they work in directly or indirectly (through environmental considerations) affect the Earth on which we live.
Contained within the Subsurface Flow Module are a number of tailor-made interfaces describing certain physics for the modeling of flow and other phenomena in subterranean environments. Known as physics interfaces, they can be combined and directly coupled to other physics interfaces within the Subsurface Flow Module, or with physics interfaces within any of the other modules in the COMSOL Product Suite. This includes coupling the poroelastic behavior described by the Subsurface Flow Module to nonlinear solid mechanics applications for soil and rock in the Geomechanics Module.
COMSOL gives you the flexibility to enter any arbitrary equations within the edit fields in The Subsurface Flow Module’s physics interfaces, which can be useful for defining geochemical reaction rates and kinetics in the interfaces for material transport. Yet, coupling these physics interfaces with the Chemical Reaction Engineering Module means that you can model many multi-species reactions with the easy-to-use physics interfaces for defining chemical reactions that this module contains. Integrating these two products is very useful for modeling the many reaction steps involved in the spread of nuclear waste from their repositories over thousands of years.
This example demonstrates how to model a phase change and predict its impact on a heat transfer analysis. When a material changes phase, for instance from solid to liquid, energy is added to the solid. Instead of creating a temperature rise, the energy alters the material’s molecular structure. Equations for the latent heat of phase changes appear in many texts but their implementation is nonstandard. Heat consumed or released by a phase change affects fluid flow, magma movement and production, chemical reactions, mineral stability, and many other earth-science applications.
This 1D example uses the Heat Transfer in Porous Media interface from the Heat Transfer Module to examine transient temperature transfer in a rod of ice that heats up and changes to water. In particular, the model demonstrates how to handle material properties that vary as a function of temperature.
This model proceeds as follows. First, estimate the ice-to-water phase change using the transient conduction equation with the latent heat of fusion. Next, compare the first solution to estimates that neglect latent heat. Finally, run additional simulations to evaluate impacts of the temperature interval over which the phase change occurs.
The Poroelasticity interface couples Darcy’s law and solid mechanics to assess deformation of porous media that results from fluid withdrawals.
The model builds on top of the Terzaghi Compaction example. Results from Terzaghi compaction and Biot poroelasticity analyses are compared to each other and are a good match to published analyses.
This non-conventional model of porous media flow utilizes creeping (Stokes) flow in the interstices of a porous media. The model comes from the pore-scale flow experiments conducted by Arturo Keller, Maria Auset, and Sanya Sirivithayapakorn of the University of California, Santa Barbara. The geometry used in the model was produced by scanning electron microscope images.
In this example, we take one of the 2D micromedia images of Keller, Auset, and Sirivithayapakorn and solve for velocities and pressures of pore fluids using the Stokes equations for Cartesian coordinates. Boundary integration is used to quantitatively evaluate fluxes.
The ability to describe how fluids funnel into tiny perforations oriented about a well bore is the subject of a rapidly growing number of analyses. In that the perforations are isolated piercings as opposed to rings, the flow field is not suited for axisymmetric analyses – fully 3-D simulations are required.
This application allows to simulate the Darcy flow to a perforated wellbore for different well, reservoir, and fluid properties to predict the fluid intake at each single perforation. It anylzes a well with up to ten perforations of different sizing in reservoirs with different properties. The application calculates the pumping rates for each perforation and visualizes the flow field in the reservoir and pressure distribution on the well.
This is a tutorial model of the coupling between flow of a fluid in an open channel and a porous block attached to one of the channel walls. The flow is described by the Navier-Stokes equation in the free region and a Forchheimer-corrected version of the Brinkman equations in the porous region.
This example treats the modeling of sub-surface flow where free convection in porous media is analyzed. The results are compared with published literature in the field.
The model couples the momentum balance to an energy balance through an equation, dependent on temperature, being directly typed into the source term for the momentum balance. This shows COMSOL Multiphysics’ unique equation-based modeling abilities and can be considered as a benchmark model for COMSOL Multiphysics capabilities in single-phase porous media flow.
Multilateral wells—those with multiple legs that branch off from a single well—can produce oil efficiently because the legs can tap multiple productive zones and navigate around impermeable ones. Unfortunately, drilling engineers must often mechanically stabilize multilateral wells with a liner or casing, which can cost millions of dollars. Leaving the wellbore uncased reduces construction costs, but it runs a relatively high risk of catastrophic failure both during installation and after pumping begins.
The poroelastic simulations estimate 3D compaction related to pumping by taking subsurface fluid flow with Darcy’s law and coupling it to structural displacements with a stress-strain analysis. This model focuses on elastic displacements brought on by changing fluid pressures when pumping begins.
Density variations can initiate flow even in a still fluid. In earth systems, density variations can arise from naturally occurring salts, subsurface temperature changes, or migrating pollution. This buoyant or density-driven flow factors into fluid movement in salt-lake systems, saline-disposal basins, dense contaminant and leachate plumes, and geothermal reservoirs, to name just a few.
This example benchmarks a time-dependent buoyant flow in porous media. Known as the Elder problem, it follows a laboratory experiment to study thermal convection. The Elder problem examines the concentrations through the coupling of two physics interfaces: Darcy’s Law and Solute Transport.
Aldicarb is a commercial pesticide, used on a variety of crops, including cotton, fruits, potatoes, and beans. This arises in the possibility that the general population may be exposed to aldicarb through the ingestion of contaminated water and foods.
This example looks at the degradation kinetics of aldicarb and its toxic by-products, investigating both the degradation time-scale as well as the spatial concentration distribution of toxic components.
In the first model the chemicals are contained in a water pond, treated as a perfectly mixed system. The second model tracks the detailed distribution of chemicals in soil as the pesticide leaches out of the pond and is transported in water through the ground.
In this example water ponded in a ring on the ground moves into a relatively dry soil column and carries a chemical with it. As it moves through the variably saturated soil column, the chemical attaches to solid particles, slowing the solute transport relative to the water. Additionally the chemical concentrations decay from biodegradation in both the liquid and the solid phase.